In the fast-paced world of financial markets, quantitative analysis plays a crucial role in informing trading decisions and strategies. Regression analysis is a powerful tool in a quantitative trader's arsenal, which allows for exploring relationships between variables and predicting future outcomes. This blog post delves into the realm of regression analysis using the weekly closing prices of the S&P 500 index as the dataset. By leveraging regression output and statistical measures, valuable insights into market trends are uncovered, along with an exploration of how traders can use confidence limits derived from regression analysis to reinforce their short-term trading strategies. This journey bridges the gap between statistical analysis and practical trading applications in the dynamic world of finance.
Why Linear Regression?
When quantitative traders are primarily
interested in forecasting the S&P 500 closing values based on the passage
of time, it would be more straightforward to create a linear regression model
using only the "Time" variable (calculated as the number of weeks
since the weekly closings) against the S&P 500 closing prices.
In this case, traders will use Time as the
independent variable and the S&P 500 closing prices as the dependent
variable in the regression model. By fitting a regression model with Time as
the predictor, traders are essentially estimating the trend or pattern in the
S&P 500 closing prices as Time progresses.
Here's how traders can create the simple
regression model:
1.
The
dataset must be organized with Time as the independent variable (predictor
variable) and the S&P 500 closing prices as the dependent variable.
2.
A
simple linear regression analysis must be run with Time as the independent
variable and S&P 500 closing prices as the dependent variable.
3.
The
regression output should be examined to understand the relationship between
Time and closing prices, paying attention to the Time coefficient to
determine the change rate over Time.
4.
The
regression equation generated by the model must be used to forecast future
closing prices based on the projected time values. The time values for the
forecast period must be input into the equation to obtain the corresponding
forecasted closing prices.
5.
The
accuracy of the model's forecasts should be assessed by comparing the predicted
closing prices to the actual values once they are available for the forecasted
period.
By using a simple regression model with Time
as the predictor, traders can focus on the trend in the S&P 500 closing
prices over Time without the need for additional variables like Open-Close,
High-Low ratios, etc.
 |
| (Click on the image to enlarge) |
Explanation of the Methodology
Here is a step-by-step summary starting from
the initial regression and then discussing how to utilize confidence limits for
trading strategies:
1. Regression Model Basics:
· Conducting
a simple regression analysis using the weekly closing prices of the S&P 500
from April 2024 to March 2025.
· Developing
a regression model using the weekly S&P 500 closing prices as the dependent
variable and Time (number of weeks since the weekly closings) as the
independent variable.
· Examining
the regression output: the coefficients for the Intercept, Time, and
statistical measures such as R-squared and significance levels.
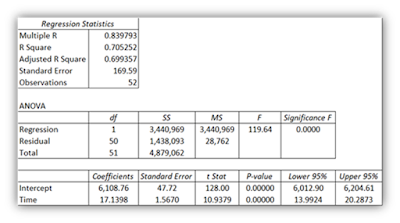
2. Regression Output:
· Intercept:
6,108.76
· Coefficient
for Time: 17.1398
· R-squared:
0.705252
· Significance
levels, standard errors, and other relevant statistical measures were examined.
· Regression
Equation: The core of the model is the regression equation: S&P 500 Price =
Intercept + (Time Coefficient * Time)
3. Forecasting Process:
· Inputting
Time: Using future "Time" values (0, 1, 2, 3, etc.) to represent the
next few weeks.
· Point
Forecast: A weekly forecast by plugging the "Time" values into the
regression equation.
4. Confidence Limits:
· Identifying
the lower and upper 95% confidence limits for the coefficients (Intercept and
Time) in the regression output.
· Lower
95% Confidence Limit: Indicating the lower boundary within which the actual
value of the coefficient is likely to fall with 95% confidence.
· Upper
95% Confidence Limit: Indicating the upper boundary within which the actual
value of the coefficient is likely to fall with 95% confidence.
5.
Applying Confidence Limits (Example):
· Week
1 (Time = 0):
o Lower Bound: 6108.76 + (13.9924 * 0) = 6108.76
o Upper Bound: 6108.76 + (20.2873 * 0) = 6108.76
o Range: 6108.76 to 6108.76 (In this case, the
range is the same because multiplying by 0 eliminates the effect of the
coefficient)
· Week
2 (Time = 1):
o Lower Bound: 6108.76 + (13.9924 * 1) = 6122.75
(approximately)
o Upper Bound: 6108.76 + (20.2873 * 1) = 6129.05 (approximately)
o Range: 6122.75 to 6129.05
· Week
3 (Time = 2):
o Lower Bound: 6108.76 + (13.9924 * 2) = 6136.75
(approximately)
o Upper Bound: 6108.76 + (20.2873 * 2) = 6149.33
(approximately)
o Range: 6136.75 to 6149.33
· Week
4 (Time = 3):
o Lower Bound: 6108.76 + (13.9924 * 3) = 6150.75
(approximately)
o Upper Bound: 6108.76 + (20.2873 * 3) = 6169.61
(approximately)
o Range: 6150.75 to 6169.61
By integrating the findings from the
regression analysis with confidence limits into trading strategies, traders can
implement a data-driven approach to managing risk and optimizing profit-taking
in their trading activities. This methodology emphasizes the importance of
combining statistical analysis with market knowledge to enhance trading
decisions in the short term.
Trading Strategy Implementation
Quantitatively savvy traders can use
the lower and upper 95% confidence limits as stop-loss and take-profit levels
for existing trades. These confidence limits provide a range within which the
actual values of the dependent variable (in this case, S&P 500 prices) are
likely to fall. Using these confidence limits as stop-loss and take-profit
levels can help traders set trade boundaries based on statistical
analysis.
Here's how traders could potentially utilize
the lower 95% and upper 95% confidence limits:
1. Stop-Loss Level (Lower 95% Confidence
Limit): If a trader is
holding a long position in the S&P 500, and the current price approaches the
lower 95% confidence limit (e.g., if the price is close to or falls below the
lower bound, it could signal a potential downside risk. In such a scenario, the
trader may consider setting a stop-loss order at or just below the lower limit
(similar to the technical support level) to limit potential losses if the price
continues declining.
2. Take-Profit Level (Upper 95%
Confidence Limit):
Conversely, if a trader is holding a position in the S&P 500 and the
current price is nearing the upper 95% confidence limit (e.g., close to or
above the upper bound) but is unable to breakout (similar to the technical
resistance level), it indicates a potential upside risk. In this case, the
trader may consider setting a take-profit order at or below the upper
limit to secure profits if the price reaches that level.
Using confidence limits as stop-loss and
take-profit levels can give traders a quantitative and statistically driven
approach to managing risk and locking profits. However, it's essential to
consider other factors, such as market conditions, trend analysis, and overall
risk management strategies, in conjunction with statistical analysis to make
well-informed trading decisions.
Suitability of the Strategy for Long-term Investors
While using confidence limits as stop-loss and
take-profit levels can be valuable for short-term quantitative traders looking
to manage risk and secure profits in the near future, their application may not
be as relevant for long-term investors with a different investment horizon and
approach. Here are some reasons why:
1. Time Horizon: Long-term investors typically have an
investment horizon ranging from several years to decades, focusing on the
fundamentals of the asset and its growth potential over the long term. In
contrast, short-term quantitative traders aim to capitalize on short-term price
movements based on statistical analysis and market trends.
2. Volatility and Noise: Short-term price fluctuations and
market volatility can cause the price to move within the confidence limits
frequently, leading to frequent stop-loss and take-profit triggers for
short-term traders. Conversely, long-term investors may be more concerned with
the overall trend and sustainable asset growth than short-term fluctuations.
3. Risk Tolerance: Long-term investors often have a
higher tolerance for market fluctuations and are willing to withstand
short-term price movements in anticipation of long-term gains. They may not be
as focused on setting precise stop-loss or take-profit levels based on
statistical confidence limits.
4. Fundamental Analysis: Long-term investors typically base
their investment decisions on fundamental analysis, focusing on factors such as
company performance, industry trends, economic indicators, and qualitative
aspects of the asset. Statistical confidence limits derived from regression
analysis may not directly align with the fundamental factors considered by
long-term investors.
In summary, while using confidence limits as
stop-loss and take-profit levels can benefit short-term quantitative traders
seeking to optimize trading strategies, it may not be the primary approach for
long-term investors focused on fundamental analysis and a buy-and-hold strategy
over an extended period. Each approach caters to different investment goals,
risk profiles, and time horizons.
Conclusion
In the trading world, the marriage of statistical analysis and
market knowledge can be potent for making informed decisions and managing risk
effectively. Exploring regression analysis and applying confidence limits as
stop-loss and take-profit levels sheds light on the intersection of quantitative
methods and trading strategies. By harnessing the insights gleaned from
regression output and confidently setting boundaries for their trades, traders
are better equipped to navigate the complex landscape of financial markets with
greater precision and confidence. As the discussion concludes, traders are
encouraged to embrace the power of regression analysis and statistical tools as
valuable resources in their quest for trading success. It underscores that
knowledge is power in quantitative trading, and data-driven decisions pave the
way to profitable outcomes.
Disclaimer:
The information provided in this blog post is for educational and informational
purposes only. While the content explores the application of regression
analysis and confidence limits in trading strategies, it is not intended as
financial advice or a recommendation for specific trading actions. Trading in
financial markets carries inherent risks, and individuals should conduct
thorough research, consider personal financial goals and risk tolerance, and
seek professional advice before making any trading decisions. Statistical
analysis and confidence limits in trading strategies should be cautiously
approached and may not guarantee successful outcomes. The author and platform
disclaim any responsibility for the outcomes of trading decisions made based on
the content presented in this blog post.
Sid's Bookshelf: Elevate Your Personal and Business Potential



No comments:
Post a Comment